Ohjeet

Aktiviteetti 1: paperin taittelu

Taita A4-paperi kahtia. Huomauta, että siinä on nyt kaksi kerrosta. Anna lapsen taittaa paperi uudestaan kahtia. Kysy lapselta, montako kerrosta siinä nyt on.

Kysy lapselta, montako kerrosta siinä tulee olemaan seuraavan taiton jälkeen. Anna hänen taittaa ja laskea. Toistakaa kunnes paperia ei saa enää taitettua.

Kerrosten määrä on yllättävän hankala laskea, koska kaikki reunat eivät ole näkyvissä ulospäin. Jos teille muodostuu erimielisyys siitä, montako kerrosta paperissa on, voitte selvittää asian tarkasti: tehkää reikä kerrosten läpi, avatkaa paperi ja laskekaa, montako reikää paperiin on syntynyt.

(Reiän tekeminen ei ole aivan helppoa, jos paperissa on monta kymmentä kerrosta! Reiän voi tehdä painamalla saksien päätä paperia kohden ja pyörittämällä sitä muodostuvassa reiässä, jolloin terä poraa paperia hiljalleen. Tämä voi vaatia hieman voimaa, tarkkaavaisuutta ja pitkäjänteisyyttä, joten operaatio on hyvä jättää vanhemman hoidettavaksi.)

Kysy myös, montako kerrosta paperissa olisi, jos sen saisi taitettua yhteensä kymmenen kertaa. Entä kaksikymmentä kertaa?

Aktiviteetti 2: hammastikkurakennelma

Laita pöydälle yksi hammastikku. Laita sen jälkeen kaksi tikkua lisää pöydälle niin, että niiden toinen pää koskettaa vanhan tikun päätä. Vanha tikku “haarautuu” kahdeksi uudeksi tikuksi. Jatka tätä: haarauta uudet tikut.

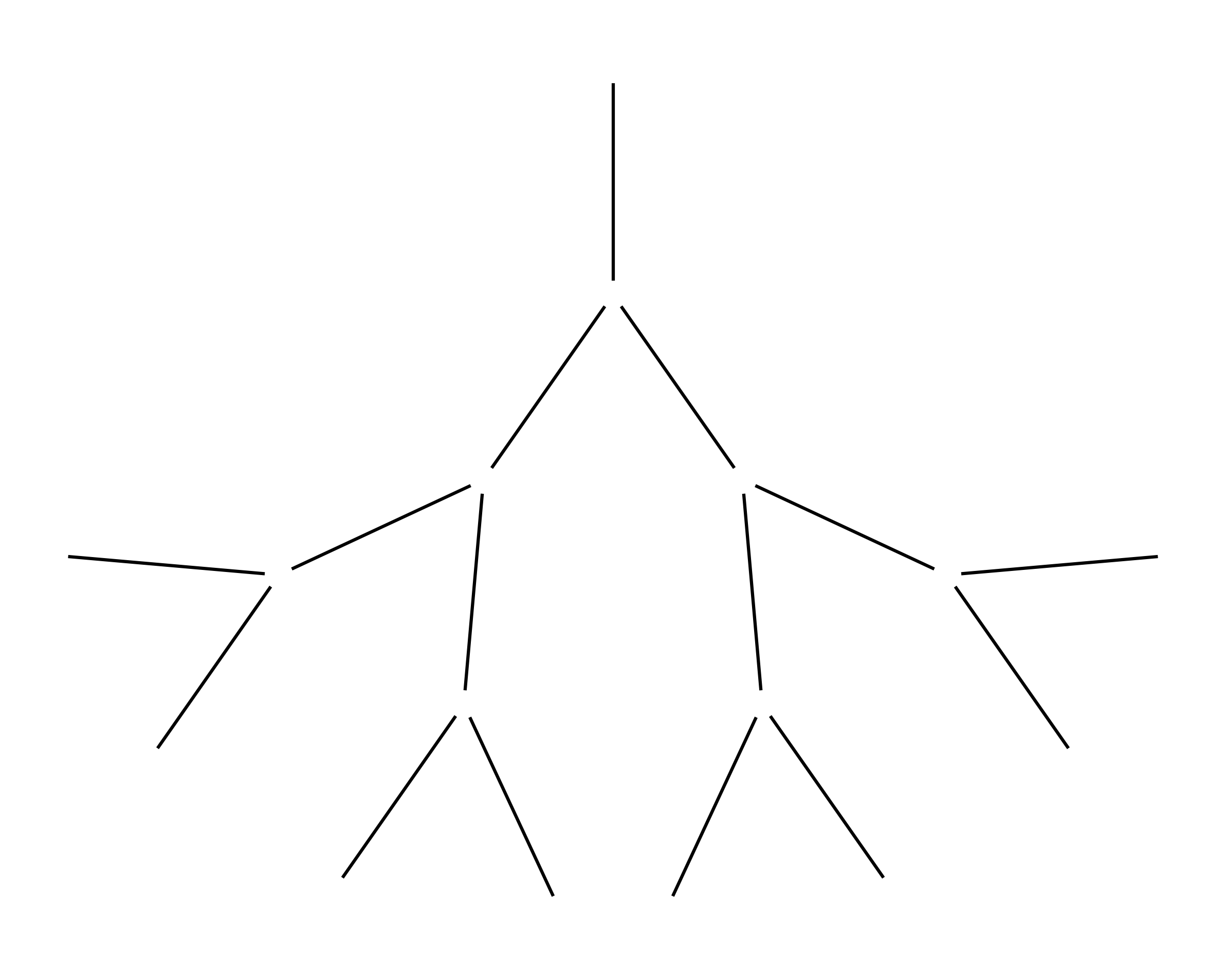
Kysy lapselta, kuinka monta tikkua seuraavissa kerroksissa tulee olemaan.

Kysy myös, kuinka monta tikkua rakennelmassa on yhteensä ja kuinka tämä määrä kasvaa, kun kerroksia tulee lisää.

Voit myös kokeilla muunnelmaa, jossa vanha tikku haarautuu aina kolmeksi uudeksi tikuksi.

Selitys

Joissakin tilanteissa lukumäärät kasvavat nopeasti suuriksi: “joka kerta tuplaantuu”, ei “joka kerta lisätään yksi”. Tätä kutsutaan eksponentiaalisuudeksi.

Helpoin esimerkki eksponentiaalisesta jonosta on jono

\[1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, \ldots,\]

jossa seuraava luku on kaksinkertainen edelliseen nähden. Tämä lukujono tulee vastaan paperin taittelussa ja hammastikkurakennelmassa.

Eksponentiaaliset jonot kasvavat nopeasti. Kymmenen taiton jälkeen A4-paperissa olisi 1024 kerrosta ja kahdenkymmenen jälkeen hieman yli miljoona ($1\ 048\ 576$)!

Voit näyttää, miten eksponentteja eli potenssilaskua merkitään: $2^5$ on sama kuin $2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2$, eli kakkosia kerrotaan keskenään viisi kappaletta.

Hammastikkurakennelmassa tikkujen kokonaismäärä on, tikkujen haarautuessa kahteen, yksi vähemmän kuin seuraavan kerroksen määrä. Esimerkiksi

\[1 + 2 + 4 + 8 = 15 = 16 - 1.\]

Tämän säännönmukaisuuden voi huomata, jos pitää kirjaa yksittäisten kerrosten määräistä ja kokonaismääristä. Sen pätevyyden voi järkeillä monella tavalla.

(Yksi tapa: lisää yksi ylimääräinen hammastikku ensimmäisen kerroksen tikun viereen. Ensimmäisessä kerroksessa on nyt yhtä paljon tikkuja kuin toisessa. Yhdistä ne. Yhdistelmäkerroksessa on yhtä paljon tikkuja kuin seuraavassa. Yhdistä ne edelleen ja toista. Lopulta huomataan, että viimeisessä kerroksessa on yhtä paljon tikkuja kuin sitä edeltävissä oli yhteensä, lukuun ottamatta alussa lisättyä ylimääräistä hammastikkua.)

Jos tikut jakautuvat kolmeen, kerroksissa olevien tikkujen määrät aina kolminkertaistuvat:

\[1, 3, 9, 27, 81, 243, 729, 2187, 6561, \ldots\]

Rakennelman tikkujen yhteismäärä on aina yksi vähemmän kuin seuraavan kerroksen määrä, jaettuna kahdella. Esimerkiksi

\[1 + 3 + 9 + 27 = 40 = \frac{81 - 1}{2}.\]

Tätä on paljon hankalampi huomata tai perustella.

(Mutta sen voi perustella esimerkiksi näin: ota viimeinen kerros erilleen muista. Tuplaa muiden kerrosten tikkujen määrät. Lisää ensimmäiseen kerrokseen yksi ylimääräinen tikku. Nyt ensimmäisessä kerroksessa on $3$ tikkua. Kun sen yhdistää seuraavan kerroksen kanssa, on tikkuja $9$. Kun nämä kerrokset yhdistää seuraavan kanssa, on tikkuja $27$ ja niin edelleen.)